kladd

En sannsynlighetsfordeling er et matematisk begrep som benyttes for beskrive hvordan stokastiske variabler fordeler seg. En stokastisk variabel kan representere mange forskjellige fenomener, det vanligste eksempelet er antallet øyer på en terning, men det kan representere vekt til en person. De enkelte utfall av en stokastisk variabel kan ikke forutsies, men sannsynlighetsfordelingen vil beskrive sannsynligheten for at hvert mulige utfall vil inntre, og hvordan verdiene i et større utvalg normalt vil fordele seg. For eksempelet med vekt vil man ikke kunne si nøyaktig vekten til en enkelt person men kan si noe om sannsynligheten for vekten til personen.

Det finnes flere forskjellige sannsynlighetsfordelinger og hvilke sannsynlighetsfordeling en variabel har er avhengig av den underliggende fysiske prosess eller logiske mekanisme; Utfallet av et terningkast, en lotteritrekning, radioaktiv nedbrytning, en intelligenstest eller ventetider i fergekø vil derfor ha forskjellige sannsynlighetsfordelinger. Dette gjør at sannsynlighetsfordelingen kan gi et hint om den underliggende prosessen.

Sannsynlighetsfordelingen av BMI hos mennesker er log-normal for 95% av mulige verdier.(1,2). For den øverste 5% av  BMI er fordelingen mest lik en potenslov fordeling(power-law).

log-normal fordelingen er storebroren til normalfordelingen som de fleste som har tatt et fag innen statistikk har vært innom. Under er en figur som illustrerer hvordan normalfordelingen ser ut

Normal fordelingen oppstår nå man har en stokastisk variabel som er en sum av mange uavhengige hendelser. For eksempel vil en Stokastisk variabel X som er summen av 10 terningkast t være tilnærmet normalfordelt

X = t1 + t2 + t3 + t4 + t5 +t6 + t7 + t8 + t9 + t10

log-normal fordeling oppstår når man har en stokastisk variabel som er produktet av mange uavhengige hendelser. For eksempel vil en stokastisk variabel Y som er produktet av 10 terningkast t være tilnærmet log-normal.

Y= t1*t2*t3*t4*t5*t6*t7*t8*t9*t10

Under er eksempler på hvordan en log-normal funksjon ser ut:

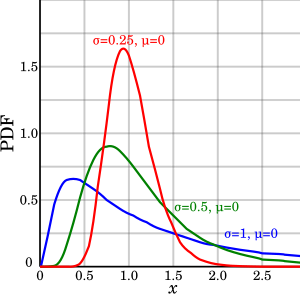
Matematisk er det en tett kobling mellom normalfordelingen og log-normal fordelingen. Dersom man tar logaritmen av en log-normalfordeling vil man ende opp med en normalfordeling. Dette kommer av at når man tar logaritmen går man fra multiplikasjon til addering. Et eksempel er vist under:

Log(A*B) = Log A + Log B

Når man tar logaritmen av den stokastiske variabel Y fra eksempelet over får man følgende:

log(Y)= log(t1*t2*t3*t4*t5*t6*t7*t8*t9*t10)

log(Y) = log(t1) + log(t2) + log(t3) + log(t4) + log(t5) + log(t6) + log(t7) + log(t8) + log(t9) + log(t10)

Fra dette blir det klar at normalfordeling og log-normalfordelingen i utgangspunktet er den samme fordelingen, bare at den er transformert med en logaritmisk funksjon. Fra dette gir også navnet log-normal mer mening.

Log-normal fordelingen går igjen på svært mange områder. Spesielt vanlig er det at lognormal fordelingen oppstår på områder der alle verdien er større enn 0. For eksempel volum, vekt, konsentrasjon, intensitet, pris eller andre empiriske verdier.  Log-normal forelingen oppstår når man har prosesser som følger Gibrats lov. Gilbrat var økonom og oppdaget at den prosentvise veksten til selskaper var uavhengig av den absolutte størelsen og denne egenskapen fører til at størrelsen på selskaper er log-normalfordeling.  Innen biologi kalles dette en multiplikativ prosess og beskriver hvordan en organisme vokser. Dersom vi starter med en organisme med størrelse X0. For hvert tidsintervall kan organismen vokse eller minke i henhold til en stokastisk variabel Fj, slik at

Xj=FjXj-1

Den grunnleggende antakelsen her er at veksten er uttrykt som en en prosent av den eksisterende vekten. Vekten etter 10 tidsperioder kunne da vært uttrykt som:

X10=F10*F9*F8*F7*F6*F5*F4*F3*F2*F1*X0

Ved å ta logaritmen på begge sider vil man få en normal fordeling som vist over. Forutsetningen er F oppfyller kravene som følger store talls lov(central limit theorem).  Med dette kreves at logaritmen av F må være uavhengig, ha lik sannsynlighetsdistribusjon og må ha et tallfestet gjennomsnitt og varians.

Det har vist seg at størrelsen til alle organismer fra encellede bakterier til mennesker er log-normal fordelt. (1)

Figuren under viser vektfordeling blant kvinner i egypt over tid. Vi ser at fordelingen har en typisk lognormal fordeling.  Vi ser at egypt har mange som er overvektige og at  vekten går opp. En annen ting som er er verdt å merker seg at

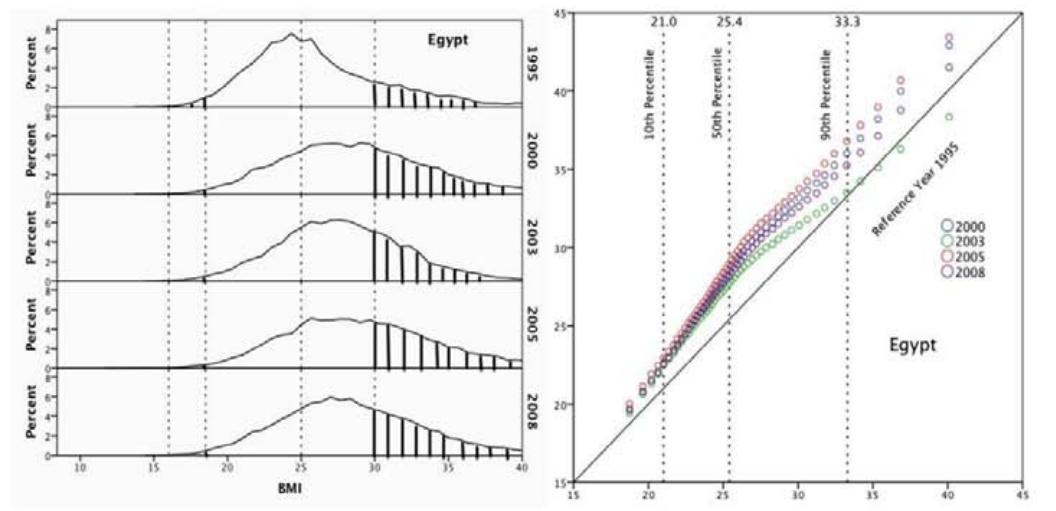
Kilde:http://journals.plos.org/plosmedicine/article/asset?id=10.1371/journal.pmed.1001367.PDF

 

 

http://economistatlarge.com/r-guide/arithmetic-harmonic-geometric-means-r

http://stat.ethz.ch/~stahel/talks/lognormal.pdf

http://projecteuclid.org/download/pdf_1/euclid.im/1089229510